
We talk and hear a lot about Regression everywhere we go. So let us skip that. In this article, we shall assume that we are masters of Regression and we have already completed building a Linear Regression Model on a given dataset.
Now, from the model, you come to notice that it has Overfit — Overfitting is a term used in data science to describe when a statistical model fits its training data perfectly and the algorithm is unable to perform accurately against unknown data, negating the goal of the method. Now this Overfitting could be because the model is too complex. This complexity will have to be reduced to improve the model and remove Overfitting.
To do this we can either decrease the magnitude of some of the Regression Coefficients and/or we could drop some of the features that do not add significant value to the final prediction. The process we will be applying to achieve this is called Regularization.
So we have come to the end of this article. Thank you.
Lol, just kidding. Well, that’s how most articles on this topic go anyway. But trust me, this one is going to be different. Let me take you through the complete experience — starting with understanding why and where we need it, its statistical importance and also how we implement it on Python.
Understanding Bias and Variance
Let us get to the basics once more — Bias and Variance.
We say that a model’s Bias is high when the model performs poorly on the training dataset. The Variance is said to be high when the model performs poorly on the test dataset. Let me give you an example to make it more clear.
Scenario 1:
Assume you are preparing for an exam (Yes, please assume.) and you read answers only for 5 questions at the end of the chapter. With this, you will be able to answer very well if the exam has the same 5 questions you prepared for. But you will fail to answer other questions that have been asked in the exam. This is an example of Low Bias and High Variance.
Scenario 2:
But in another scenario, let us say that you have prepared for the exam by actually going through the entire chapter and understanding the concepts instead of memorizing the answers to 5 questions. With this, you will be able to answer any question that comes in the exam but you will not be able to answer it exactly as given in the book. This is an example of High Bias and Low Variance.
So now, coming back to Data Science terminologies — It is important to understand that there is always going to be a trade-off between Bias and Variance in any model that you build. Take a look at this graph that shows Variance and Bias for different Model Complexities. A model with Low Complexity or a Simple Model would have High Bias and Low Variance and a Highly Complex Model would usually have Low Bias and High Variance. (Try relating this with the Exam example I gave above.) Also, note that the Total Error (Bias + Variance) of the model in the case of both a very Simple Model and a highly Complex Model will be Maximum.
So it is now safe to say that we would be needing a model to be built that has the Lowest Total Error — A model that is capable of identifying all the patterns from the Train Data and also performing well on data it has not seen before i.e. Test Data.
How does Regularization help with Model Complexity?
Regularization comes into the picture when we need to take care of the model complexity to balance Bias-Variance. Regularization helps decrease the magnitude of the model coefficients towards 0 (can also help in completely removing the feature from the model when coefficient become 0) thus bringing down the model complexity. This will in turn reduce the overfitting of the model and bring down the Total Error — exactly what we wanted to achieve.
Consider the Ordinary Least Squares (OLS Regression) — the Residual Sum of Squares or the Cost Function is given by:
When we build a Regression Model, we construct the feature coefficients in such a way that the Cost Function or the RSS is minimum. Note that this RSS takes into account only the Bias that comes out of the model and not the Variance. So the model may try to reduce the Bias and overfit the training dataset — Which will result in the model having High Variance.
Hence, Regularization comes into helping us here by modifying the Cost Function of the model a little to reduce the model complexity and thereby reducing Overfitting.
So how do we actually do it?
In Regularization, we add a Penalty term to the Cost Function that will help us in controlling the Model Complexity.
After Regularization, Cost Function becomes RSS + Penalty i.e. we add a Penalty term to the regular RSS in the cost function.
Ridge Regression
In Ridge Regression, we add a penalty term which is lambda (λ) times the sum of squares of weights (model coefficients).
Note that the penalty term (referred to as the Shrinkage Penalty) has the sum of squares of weights. So in Regression, we build the model by trying to reduce the Cost Function. Hence, here the model will try to reduce the model coefficients(weights) to reduce the Cost Function thereby reducing the Model Complexity.
Let us now understand what lambda (λ) does here. λ is the Tuning Parameter. Assigning 0 to λ will make the entire Penalty Term 0 and the model coefficients will not be reduced (No Shrinkage) leading to Overfitting. But when λ reaches very high values, the Penalty Term also increases thus bringing down the model coefficients and might cause Underfitting.
This is why we must choose the right value of λ to make sure the Model Complexity is effectively reduced but there is no Overfitting or Underfitting. Choosing the right λ value in Ridge Regression can be done by Hyperparameter Tuning.
Please note that before performing Ridge Regression, the dataset must be Standardized. This is because we are dealing with the coefficients of the model and it will make sense if they are on the same scale.
Lasso Regression
The important difference between Ridge and Lasso Regression lies in the Penalty Term.
In Lasso Regression, we add a penalty term which is lambda times the sum of absolute values of weights (model coefficients).
The remaining principles and the way the Penalty Term brings down the model coefficients to decrease the Model Complexity remains similar to that of Ridge Regression.
But one difference that must be noted here is that in the case of Lasso Regression the Shrinkage Term(Penalty Term) forces some of the model coefficients to become exactly 0 thereby removing the entire feature from the model (given that the λ value is large enough). This gives a whole new application of Lasso Regression — Feature Selection. This is not possible in case of Ridge Regression.
Please note that similar to Ridge Regression, before performing Lasso Regression, the dataset must be Standardized. This is because we are dealing with the coefficients of the model and it will make sense if they are on the same scale.
Python Implementation of Regularization Techniques — Ridge and Lasso
The entire implementation of Ridge and Lasso regression along with a detailed analysis of a dataset starting with Exploratory Data Analysis, Multiple Linear Regression including Multicollinearity, VIF Analysis etc. can be found here.
The dataset used in this implementation is of ‘Surprise Housing Case Study’.
You can find the Github link to the Python implementation here: https://github.com/Adhithia/RegressionWithRegularization
You can edit and collaborate on the same project on Kaggle here:
https://www.kaggle.com/adhithia/regression-with-ridge-and-lasso-regularization
Snippet — Ridge Regression Implementation
That’s the end of Regression Regularization Techniques — Ridge and Lasso.
Start blogging about your favorite technologies, reach more readers and earn rewards!
Join other developers and claim your FAUN account now!
User Popularity
41
Influence
4k
Total Hits
1
Posts












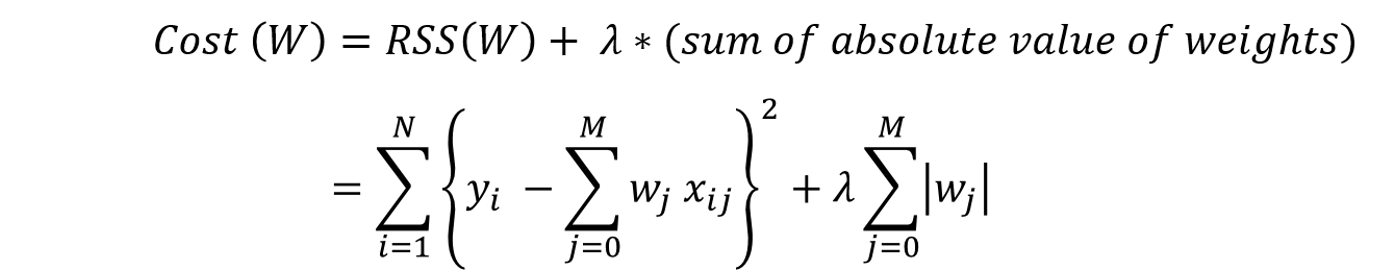







Only registered users can post comments. Please, login or signup.